Day 04 – Minkowski Distance

ลองเขียน Data Series วันละตอนเนาะ
ครบ 1 ปีเราจะมี 365 เรื่องให้อ่านกัน ^^

** English content will be available soon **

=======================
ถ้าพูดถึง พีทาโกรัส คุณนึกถึงอะไร !?
=======================

เมื่อพูดถึงพีทาโกรัส หลายคนคงร้องอี๋ 
แต่หลายๆคนกลับขอบคุณบุคคลสำคัญคนนี้
ที่ช่วยให้การประมาณค่าต่างๆเป็นเรื่องที่ง่ายขึ้นมากๆ
ถ้าใครคุ้นๆเจ้าสามเหลี่ยมมุมฉากที่เราเรียนกันตั้งแต่ ม 4
จะพบว่าทฤษฎีบทของพีทาโกรัสที่ว่าด้วย

ในสามเหลี่ยมมุมฉากใด ๆ
พื้นที่ของสี่เหลี่ยมจัตุรัส
ที่มีด้านเป็นด้านตรงข้ามมุมฉาก
เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมฉาก
ของสามเหลี่ยมมุมฉากนั้น

หรือสามารถเขียนเป็นสมการง่ายๆได้ว่า
a**2 + b**2 = c**2
โดยที่ a และ b แทนขนาดของด้านสามเหลี่ยมที่ประกอบเป็นมุมฉาก
และ c แทนขนาดของด้านสามเหลี่ยด้านตรงข้ามมุมฉาก
โดยที่แอดขอเขียนสัญลักษณ์ ยกกำลังด้วย **

ดังนั้นหากเราต้องการหาค่า c
หรือความยาวของด้านตรงข้ามมุมฉาก
เราก็สามารถทำได้ง่ายๆเพียงถอดรากที่สองของสมการ
ได้เป็น
sqrt(a**2 + b**2) = c
โดยที่ แอดขอเขียนสัญลักษณ์ การถอดรากที่สอง
ด้วยการเขียนฟังก์ชันแบบนี้ sqrt(x)

แล้วมันเกี่ยวอะไรกับการวัดระยะล่ะ !??

เราสามารถใช้ทฤษฎีบทของพีทาโกรัส
มาช่วยในการวัดสิ่งของที่มีความสูงมากๆ
เช่น ต้นไม้ ภูเขา หรือตึก
เริ่มต้นให้เรายืนทำมุม 45 องศา
กับยอดของสิ่งที่เราต้องการวัดความสูง
เช่นเราอยากวัดความสูงของตึก
เราก็เดินถอยออกมาจากตัวตึกเรื่อยๆ
จนกระทั่งแหงนหน้ามองดาดฟ้าของตึกแล้วทำมุม 45 องศา
ณ ตอนนี้เราสามารถรู้มุมแบบคร่าวๆว่าคือ 45 องศา
ระยะทางที่เราเดินมาจนแหงนหน้ามองตึกได้
และแน่นอนความสูงของตึกทำมุม 90 องศากับพื้นถนน
ได้รูปสามเหลี่ยมละ !!
หลังจากนั้นเราก็สามารถแทนค่าเพื่อหาความสูงของตึกได้

คำนวน
ตึกสูง x เมตร
ระยะห่างเรากับตึก y เมตร
ระยะระหว่างเรากับยอดตึก z เมตร
สามเหลี่ยมที่มี มุม 90 องศา และ 45 องศา
แสดงว่ามุมที่เหลือคือ 45 องศา
เพราะมุมภาพในของสามเหลี่ยมรวมกันต้องได้ 180 องศา

การที่สามเหลี่ยมจะมี 2 มุมที่เท่ากันได้
จะต้องมีด้านประกอบของสามเหลี่ยมที่มีขนาดเท่ากัน
หรือ x มีค่าเท่ากับ y
(ในกรณีนี้สามารถตอบได้เลยว่าตึกสูงเท่าไหร่ !!
โดยวัดระยะที่เราเดินห่างออกไปเรื่อยๆเท่านั้นเอง)

แต่ถ้าใช้ทฤษฎีบทของพีทาโกรัส
จะได้ว่าจากสูตรตรีโกณของ sin cos tan
โดยที่
sin(มุม) = ด้านตรงข้ามมุม / ด้านตรงข้ามมุมฉาก
cos(มุม) = ด้านที่ชิดมุม / ด้านตรงข้ามมุมฉาก
tan(มุม) = ด้านตรงข้ามมุม / ด้านที่ชิดมุม

ณ ตอนนี้เราต้องการทราบความสูงตึก
หรือด้านที่ตรงข้ามเรา
เลือกสูตร
tan(มุม) = ด้านตรงข้ามมุม / ด้านที่ชิดมุม
แทนค่า
tan(45) = ด้านตรงข้ามมุม / y

ดังนั้นความสูงของตึกจะมีค่าเท่ากับ
ด้านตรงข้ามมุม = y * tan(45)

แทนค่า
ถ้าระยะระหว่าง เรากับตึก เท่ากับ 10 เมตร
tan(45) = 1
ด้านตรงข้ามมุม = 10 * tan(45)

ดังนั้น คำตอบความสูงของตึกเท่ากับ 10 เมตรนั่นเอง 

พีทาโกรัสเกิด 582 ก่อนคริสต์ศักราช
ที่เมืองซามอส (Samos) ประเทศกรีซ (Greece)

==========================
Euclidean Distance คุ้นๆกันไหมเอ่ย !?
==========================

Euclidean Distance คือการวัดระยะ
หรือสิ่งของจากการดู Delta หรือความต่างกันของแต่ละแกน
ซึ่งคล้ายกับการคำนวณหาขนาดของ Manhattan Distance มากๆ

จากตัวอย่างเดิมของ Manhattan Distance
หรือ L1-Norm Distance
สมมติ
X มีขนาด 10 หน่วย
Y มีขนาด 5 หน่วย
เราสามารถเขียนในรูป Vector ได้ว่า
v = [ 10, 5 ]
ทีนี้ขนาดของ Vector นี้หาได้จากการหา Delta ทีละแกน
โดยทำการเทียบระยะทางกับจุดกำเนิด หรือจุด (0, 0)
จะสามารถแทนค่าสมการได้ดังนี้
(10 – 0) + (5 – 0) = 15

สังเกตได้ว่าอีกหนึ่งจุดที่เรียกวิธีนี้ว่า L1-Norm
นั่นคือการที่แต่ละพจน์ หรือแต่ละแกนที่คำนวนนั้น
ถูกยกกำลังด้วย 1
(10 – 0) + (5 – 0) = 15
เขียนใหม่ได้เป็น
(10 – 0)**1 + (5 – 0)**1 = 15**1

สำหรับ Euclidean Distance นั้น
คำนวณผ่าน L2-Norm
จากตัวอย่างเดิม
v = [ 10, 5 ]
เราสามารถหาระยะทางแบบ Euclidean Distance ได้จาก
(10 – 0)**2 + (5 – 0)**2 = || v ||**2
ทำการถอดรากที่สอง
sqrt((10 – 0)**2 + (5 – 0)**2) = || v ||

ดังนั้นหากคำนวนหาขนาดของ v แบบ L2-Norm
จะได้ค่าประมาณ 11.18

สูตรคล้ายๆกับทฤษฎีบทของพีทาโกรัสใช่ไหมเอ่ย ^^ 

งั้นเราก็สามารถเขียนสูตรใหม่ได้เป็น
sqrt((x – 0)**p + (y – 0)**p) = z
โดยที่ p = ตัวแทนของ Dimension Space !!

p = 1 จะได้ Manhattan Distance
p = 2 จะได้ Euclidean Distance

Euclidean Distance นั้นชื่อตามตัวเลยครับ
มาจากนักคณิตศาตร์ที่ชื่อ ยุคลิด
ยูคลิดเกิดที่เมืองอเล็กซานเดรีย ประเทศอิยิปต์
365 ปีก่อนคริสตกาล

================
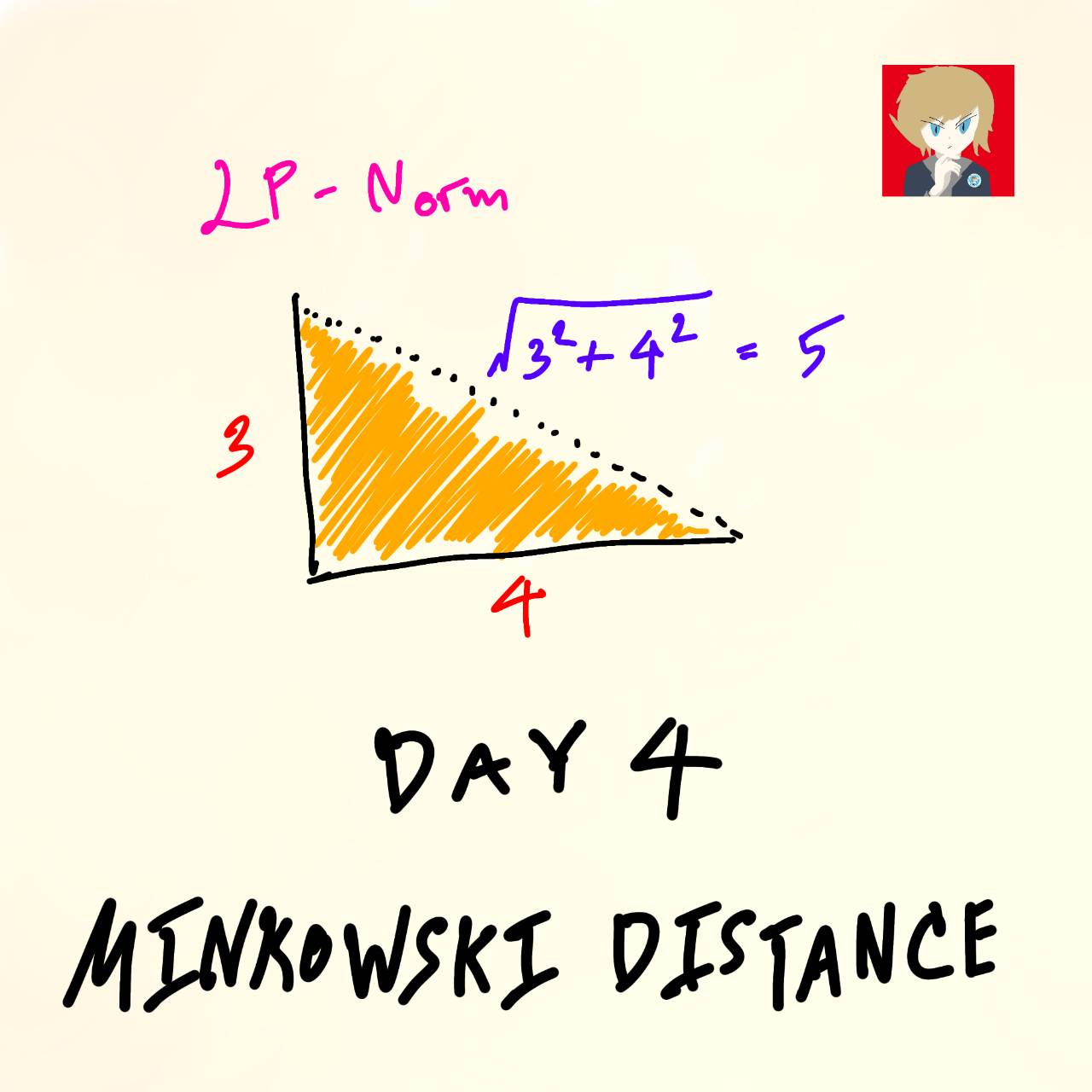
Minkowski Distance
================

เรารู้จักการวัดระยะผ่านระบบของ Function spaces
หรือ Lp-Norm
แต่สำหรับ Minkowski Distance นั้น
เพิ่มความพิเศษด้วยการยกกำลัง Delta ของแต่ละแกน
โดยยกกำลังตามจำนวนค่า Norm ที่เราต้องการ
แล้วทำการรวมค่าผลลัพธ์เข้าด้วยกัน
จากนั้นทำการถอดรากที่ได้ทำการยกกำลังไป

เช่น
หากยกกำลัง 3 ที่ทุกจุดของข้อมูล
เราก็มาถอดรากที่ 3 ในภายหลัง
แต่หากทำการยกกำลัง 10
เราก็มาถอดรากที่สิบในภายหลังเช่นเดียวกัน

ซึ่งแน่นอนว่า p นั้นสามารถไล่ไปได้ถึง Infinity !
แต่การจะเห็นภาพนั้นคงจะค่อนข้างยากหน่อย
แต่ถ้าเราค่อยๆคิดถึงระยะทางที่พาดผ่าน
ตั้งแต่
p = 1 คือระยะทางของเราที่สามารถวิ่งไปได้แค่ทีละแกนเท่านั้น
p = 2 คือระยะทางของเราที่สามารถวิ่งไปได้ทีละ 2 แกน

ดังนั้นสำหรับ p ที่มากขึ้นเรื่อยๆ
จำนวนแกนที่สามารถวิ่งได้ก็เพิ่มขึ้นเรื่อยๆ ด้วยเช่นเดียวกัน

จากตัวอย่างด้านบนเราเทียบ Vector กับจุดกำเนิด
แต่ในการใช้งานในมุมของ Data Science นั้น
เราใช้เปรียบเทียบ หรือวัดระยะห่าง
ของ 2 Vectors
โดย แต่ละ Vector เปรียบเสมือนเป็นตัวแทน ลูกค้า 1 คน
ดังนั้นเราสามารถเปรียบเทียบระยะความใกล้ หรือไกล
ของลูกค้าแต่ละคนได้โดยการหาขนาดของระยะห่างนั่นเอง

==============================
Minkowski กับการใช้งานใน Business
==============================

ตัวอย่างการคำนวณค่าความเหมือนของลูกค้าแต่ละคน
เช่น
นาย A มี vector = [2, 0, 1]
นาย B มี vector = [1, 2, 0]
นาย C มี vector = [0, 2, 1]

โดยที่ค่าใน vector นั้นเป็นตัวแทนของ Features ของลูกค้า
Features อาจจะมองว่าเป็นลักษณะของลูกค้า
ซึ่งอาจจะเป็น ส่วนสูง, น้ำหนัก, การซื้อของ
โดยที่เราจะมอง 1 Feature เปรียบเสมือนข้อมูล 1 แกน
(บางคนก็ใช้คำว่า 1 มิติ หรือ 1 column)

เอาล่ะ เริ่มคำนวณ Minkowski Distance ที่ p = 2
หรือ Euclidean Distance กัน
โดยคำนวนหา Delta ของแต่ละแกน
นาย A มีระยะห่างจาก นาย B
= sqrt((2-1)**2 + (0-2)**2 + (1-0)**2)
= 1.414 หน่วย

นาย A มีระยะห่างจาก นาย C
= sqrt((2-0)**2 + (0-2)**2 + (1-1)**2)
= 2 หน่วย

และนาย B มีระยะห่างจาก นาย C
= sqrt((1-0)**2 + (2-2)**2 + (0-1)**2)
= 1.414 หน่วย

จะได้่ผลลัพธ์ดังนี้
นาย A มีระยะห่างจาก นาย B = 1.414 หน่วย
นาย A มีระยะห่างจาก นาย C = 2 หน่วย
นาย B มีระยะห่างจาก นาย C = 1.414 หน่วย

ดังนั้นถ้าเทียบลักษณะของ ลูกค้าทั้งสามคนนี้
เราก็สามารถบอกได้ว่า
นาย A มีลักษณะใกล้เคียงกับ นาย B แต่ ไม่เหมือน นาย C
และนาย B เองก็อยู่ลักษณะใกล้เคียงกับนาย C ด้วยเช่นกัน

จะเห็นได้ว่า
ระยะห่างของ (A, B) = ระยะห่างของ (B, C)

แต่ แต่ แต่ แต่ แต่ แต่ แต่ แต่ แต่ !

เห็นอะไรไหมครับ ที่แปลกๆ
ความห่างที่ได้ออกมานั้น ถึงแม้จะมีค่าเท่ากัน
แต่มาจากการคำนวณระยะห่างของ Vector ที่มีค่าไม่เหมือนกันเลย
เพราะการคำนวณระยะห่างของระบบ Minkowski นั้น
ไม่ได้สนใจเรื่องของลำดับก่อนหลังของแกน
แต่เป็นการคิดรวมระยะห่างของทุกแกนเข้าด้วยกันเลยนั่นเองครับ

ง่ายแค่นี้เองครัช 

Minkowski เป็นชาวเยอรมันมีชีวิตในช่วง 1864-1909
เป็นทั้งนักคณิตศาสตร์ และนักฟิสิกส์
แถมยังเป็นอาจารย์ของ Einstein
และด้วย Minkowski Distance นี่เอง
นำไปสู่รากฐานของทฤษฎีสัมพันธภาพ
ที่อธิบายเรื่องราวของ Space–Time
โดยต่อมาเป็นที่รู้จักกันในชื่อ “Minkowski spacetime”

================
อธิบายศัพท์เพิ่มเติม
================

Delta คือการหาระยะห่าง
หรือความแตกต่างของข้อมูลเทียบกัน
เช่น Delta(X2, X1) คือนำ X2 มาลบ กับ X1

Gradient คืออัตราการเปลี่ยนแปลงของฟังก์ชัน
เช่น ฟังก์ชัน f(X) โดยที่ X เปลี่ยนแปลงน้อยๆ
จะได้ d(f(x)) / dx
โดยที่เรียก d(f(x)) / dx ได้อีกชื่อว่า Slope นั่นเอง
ยกตัวอย่างเช่น อัตราการเปลี่ยนแปลงของความเร็วรถ
จาก ตำแหน่ง x1 ไปยัง x2
แสดงว่าระยะทางมีการเพิ่มขึ้น = x2-x1
โดยเทียบกับ เวลาที่เปลี่ยนแปลงไปชั่วขณะหนึ่ง
และ Gradient ของความเร็วที่เปลี่ยนแปลง
ต่อ เวลาที่เปลี่ยนแปลงชั่วขณะหนึ่ง ก็คือ ความเร่งนั่นเอง

=========================
ประโยชน์ของ Minkowski Distance
=========================

อาทิเช่น
– ศึกษาและ อธิบายทฤษฏีสัมพันธภาพ
– ใช้ในระบบการแก้สมการที่มี Infinite Solution
(Underdetermined systems)
– ใช้การการคำนวณเล่นหมากรุก !
– ดูความแตกต่างของข้อมูลกลุ่ม Discrete
– ตรวจดูความแตกต่างของรูปร่างโมเลกุล
– การค้นหาคนที่มีพฤติกรรมเหมือนกลุ่มใดกลุ่มหนึ่ง
– การนำเสนอสินค้าที่ใกล้เคียงกับคนแต่ละกลุ่ม
– Classification Model เช่น KNN ใช้การวัดระยะห่างเข้ามาช่วยทำนาย
– การจัดกลุ่มลูกค้า
– หาความคล้ายกันของชื่อคน
– เช็คคุณภาพของข้อความ
– การค้นหาเอกสาร
– การค้นหา Intent ของ Chatbot
– เช็คความเหมือนกันของรูปภาพ
– การค้นหาคนที่มีพฤติกรรมเหมือนกลุ่มใดกลุ่มหนึ่ง
– การแนะนำสินค้าโดยอิงจากความใกล้เคียงกันของกลุ่ม
– การส่งแคมเปญการตลาดให้แต่ละกลุ่ม
– การทำโปรไฟลล์ลูกค้า
– ใช้เป็น 1 ใน ตัววัดประสิทธิภาพโมเดลในโจทย์ปัญหา Multilabel-Classification
– และอื่นๆอีกมากมาย

=========================
ขอบคุณทุกท่านที่ติดตามครับ
ฝากไลค์ แชร์ คอมเมนท์ เพื่อเป็นกำลังใจ
Made with Love  by Boyd
=========================

Series นี้ออกแบบมาให้เพื่อนๆที่สนใจในเรื่องของ Data หรือเพื่อนๆที่ทำงานสาย Data แต่มีเวลาจำกัดได้อ่านกันครับ โดยเนื้อหาอาจจะมีสลับกันไปทั้งในเรื่องของความง่าย และยาก รวมถึงเนื้อหาที่หลากหลายทั้ง Coding, Math, Data, Business, และ Misc
– Feedback กันเข้ามาได้นะครับ ว่าชอบหรือไม่ชอบอย่างไร เพื่อการปรับปรุง Content ให้ดียิ่งขึ้น
– หากผิดพลาดประการใดต้องขออภัยมา ณ ที่นี้ด้วยนะครับ
– ท่านใดมีประสบการณ์การใช้งาน สามารถแชร์ให้เพื่อนๆอ่านได้เลยนะครับ

#BigDataRPG#DataScienceวันละตอน#MinkowskiDistance